Problem Solving and Proofs Archives - Page 6 of 9

Math Word Problems: Solving Number Problems Part 1

September 11, 2012 GB High School Algebra, High School Mathematics, Problem Solving and Proofs

This is the first post in the Word Problem Solving Series. This series is intended for middle school students. In this post, we are going to discuss how to solve number word problems in Algebra.

The that you should observer in this series translating words into algebraic expressions and equations. Prior to the discussion of word problems, you have already learned how to solve equations, so I will not show the solution in details. » Read more

4 comments number problems, solving word problems, word problems in algebra

Mathematical Proofs Without Words: What are they?

June 1, 2012 GB Problem Solving and Proofs

In Proof of the Sum of Square Numbers, I have mentioned about proof without words. Some of you are probably wondering what they are, so I will discuss in detail.

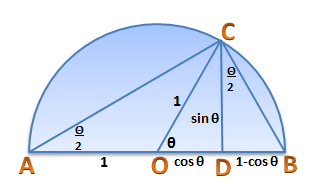
Proof without words are diagrams or pictures that help readers see why a particular statement is true even without accompanying explanations. One example is a classic proof of the Pythagorean theorem shown in the first figure.

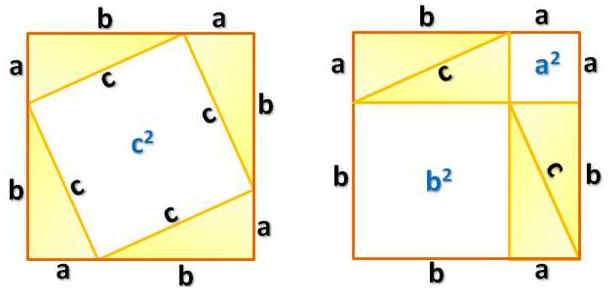
In the example, we have two congruent squares. There are four congruent right triangles occupying portions of both squares. It is clear that the total area occupied by the triangles in the first diagram is equal to the total area occupied by the four triangles in the second diagram. If the occupied areas on both squares are equal, it follows that the unoccupied areas are also equal (Why?). Therefore, 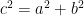$c^2 = a^2 + b^2$ . Now, that proves the Pythagorean theorem.

Proofs without words cannot always be considered as “proof” in the formal sense. For instance, the second figure cannot be considered as a proof since only four cases are shown. The generalization of the figure shows that the sum of the first $n$ positive odd integers (group the numbers by colors) is a square of its nth term or

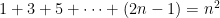$1 + 3 + 5 +\cdots + (2n - 1) = n^2$ .

The formal proof of the equation can be demonstrated using mathematical induction.

***

I am currently reading a collection of Proofs without Words by Roger Nelsen. You may want to check it out.

5 comments math proof, mathematical proof, mathematical proof without words, proof without words

The Proof of the Tangent Half-Angle Formula

May 3, 2012 GB High School Mathematics, High School Trigonometry, Problem Solving and Proofs

In this post, we prove the following trigonometric identity:

$\displaystyle \tan \frac{\theta}{2} = \frac{\sin\theta}{1 + \cos \theta} = \frac{1 - \cos \theta}{\sin \theta}$ .

Proof

Consider a semi-circle with “center” $O$ and diameter $AB$ and radius equal to 1 unit as shown below. If we let $\angle BOC =\theta$ , then by the Inscribed Angle Theorem, $\angle CAB = \frac{\theta}{2}$ .

Draw $CD$ perpendicular to $OB$ as shown in the second figure. We can compute for the sine and cosine of $\theta$ which equal to the lengths of $CD$ and $OD$ , respectively. In effect, $BD = 1 - \cos \theta$ and $AD = 1 + \cos \theta$ . » Read more