Is there an SSA Congruence?
In the Triangle Congruence post, we discussed about ways to test if two triangles are congruent. The only theorems (or sometimes called postulates) that hold are the SSS, SAS and ASA congruence. We ended our discussion with the question about the AAS (or SAA), AAA and SSA (or ASS) congruence.
Let us try to explore the AAS case. If we have two triangles (see first pair of in Figure 1), and two pairs of their angles (denoted by the blue and red circles) are congruent the third pair of angles (denoted by the yellow circles in the second pair) are also congruent. Hence, a pair of sides (both included in two pairs of congruent angles) are congruent, which is similar to the ASA congruence. Therefore AAS congruence holds and is equivalent to ASA congruence.
In Figure 2, shown are triangles with three pairs of angles that are congruent. It is clear that the two triangles are not congruent. Therefore, AAA congruence does not hold.
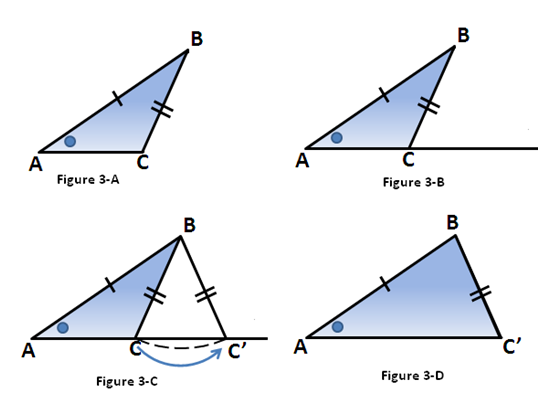
Now, let us try the SSA congruence. Figure 3-A shows triangle ABC with sides and angle marked. We extend AC to the right hand side (see Figure 3-B), then rotate BC about point B (see Figure 3-C). We let C’ be the intersection of BC and the extended segment such that BC is congruent to BC’ (see Figure 3-D).
Looking at Figure 3-A and Figure 3-D, two pairs of their sides and a pair of non-included angles are congruent, but the triangles are not congruent. Therefore, SSA (or ASS) congruence does not hold.