High School Geometry Archives - Page 18 of 23

Tessellation: The Mathematics of Tiling

March 5, 2010 GB High School Geometry, Math in Real Life

You have probably noticed that floors are usually tiled in squares or sometimes in rectangles. What is so special about these shapes? What are the disadvantages of using other shapes?

The most important thing to consider in tiling is that the shape of the tiles should cover the floor without gaps and without overlaps. Probably, this condition will be satisfied easily if the tiles that are used have the same shape and the same size.

If we are going to use regular polygons in tiling, then we can use squares, equilateral triangles or regular hexagons as shown in Figure 2. These polygons will cover the floor without gaps and overlaps, and thus will minimize the need for cutting.

Figure 1 – A honeycomb is an example of hexagonal tiling.*

In mathematics, the term used for tiling a plane (floor in our context) with no gaps and no overlaps is tessellation. Of course, we are not the only one who realized the advantages of shapes that can tessellate. The bees create honeycombs in hexagonal tessellation as shown in Figure 1.

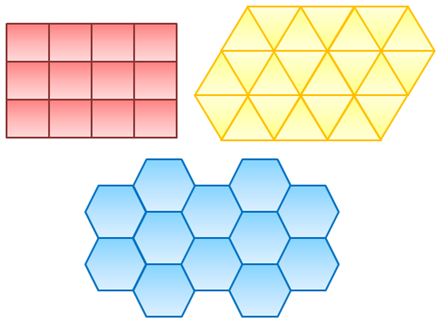
Figure 2 – Examples of regular polygons that can tile the floor without gaps and overlaps.

Note: If you are wondering how these beautiful diagrams were created, I have created a tutorial about it here.

Looking at Figure 3, we can see that not all regular polygons exhibit the property shown by polygons in Figure 2. It is clear that the regular polygons namely pentagons, heptagons and octagons do not tessellate the plane.

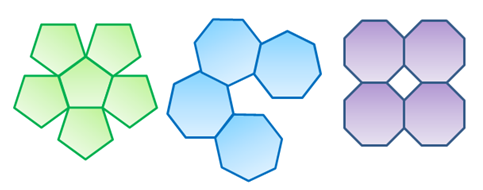
Figure 3 – Examples of polygons that cannot tessellate the plane.

From the discussion above, we want to ask the following questions:

What are the properties of polygons that can tessellate the plane?
Aside from equilateral triangles, squares and regular hexagons, what other polygons can tessellate the plane?

Delving Deeper

In Figure 4, notice that in order for a regular polygon to tessellate the plane, the sum of the interior angles that meet at a common point must equal 360 degrees.

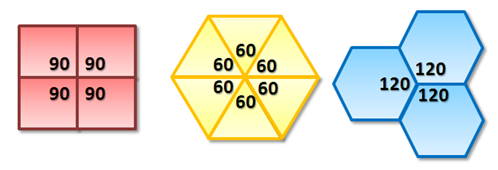
Figure 4 – The Interior angles of polygons that can tessellate the plane add up to 360 degrees.

On the other hand, the three polygons in Figure 5 do not tessellate the plane. In the leftmost illustration, the measure of the interior angles of a regular pentagon is 108 degrees. If we try to tile the plane, we can see that the measure of the three angles meeting at a common point add up to 324 degrees. Now, this leaves an “exterior angle” of 36 degrees angle as shown. In the remaining part of this article, we will refer to this type of angle (denoted by red text measurements) as exterior angles.

As we increase the number of sides of a regular polygon, we also observe that we cannot make three interior angles meet at a common point without overlapping. This is shown in the center and rightmost illustration in Figure 5. Only two polygons can have their vertices attached at a common point without overlapping.

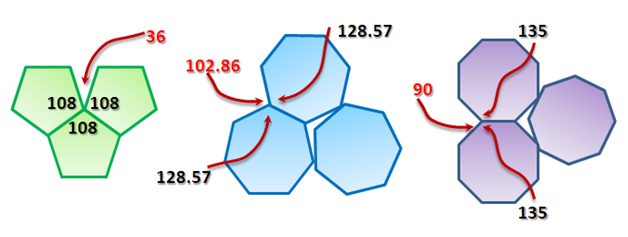
Figure 5 – Exterior angles produced by some polygons.

In the Angle sum of Polygon post, we have discussed that the sum of the interior angles of a polygon with $n$ sides is described by the formula $180(n-2)$ . Since we have $n$ congruent angles, it follows that each angle measures $\displaystyle\frac{180(n-2)}{n}$ . As a consequence, as the value of $n$ increases, the measure of the interior angles increases. In effect, the measure of the exterior angle decreases as the value of $n$ increases.

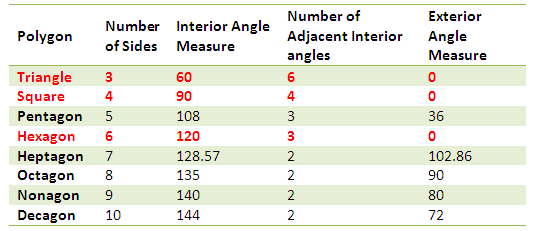
Figure 6 – Table showing properties of tessellating and non-tessellating polygons.

Looking at the table in Figure 6, we can see that polygons whose product of interior angles and the number of adjacent vertices is 360 tessellate. Consequently, the measure of their exterior angles is 0.

Furthermore, observe that as the number of sides of the polygons increases, the fewer the number of vertices that we can fix at a common point without the polygons overlapping. Since all regular polygons with more than six sides have interior angles measuring greater than 120 degrees, placing their three interior angles at a common point will make two of them overlap. This is because their angle sum would be greater than 360 degrees (we can verify this using the Tessellation GeoGebra applet).Thus, for polygons more than six sides, only two vertices can be placed adjacently without overlapping. Now, to tessellate, the two adjacent interior angles of these polygons must add up to 360 degrees, which means that each of them must equal 180 degrees. Of course, there is no such polygon. Hence, there is no way that we can tessellate the plane with regular polygons having number of sides greater than six. This proves that the only regular polygons that we can use to tessellate the plane are the three polygons shown in Figure 2.

Non-Regular Tessellations

We will not limit, of course, our creativity by using only regular polygons in tiling floors. The polygons shown in Figure 7 are some of the tiles which are not regular polygons. In the rightmost figure, we used octagons and squares in tiling, which is considered as a semi-regular tessellation.

Figure 7 – Example of non-regular polygon tessellation.

Going Beyond

Not all tessellations are created in the Euclidean plane. In the leftmost illustration in Figure 8, the sphere is tessellated by a truncated icosidodecahedron.

Figure 8 – Tiling in the Spherical, Hyperbolic and Euclidean Plane**.

The center illustration is an example of tessellation of the hyperbolic plane, created by M.C. Escher and the rightmost illustration is another example of the tessellation of the Euclidean plane – a lso by M.C. Escher.

**********************************************************************

Photos used in this article:

*Buckfast Bee ”Source:”’ picture taken by Frank Mikley on 2006-07-23. Adapted from the Wikimedia Commons file “Image:Buckfast_bee.jpg” http://upload.wikimedia.org/wikipedia/commons/1/1e/Buckfast_bee.jpg

**1. Spherical truncated Icosidodecahedron .Adapted from the Wikimedia Commons file “Image: Uniform_tiling_532-t012.png”

http://upload.wikimedia.org/wikipedia/en/5/55/Uniform_tiling_532-t012.png

**2. Circle Limit III by M. C. Escher (1959).

**3. Angles and Devils by M. C. Escher (1941).

22 comments floor tiling, regular tessellations, semi-regular tessellations, sum of interior angles, truncated icosidodecahedron

CaR Tutorial 2 – The MidSegment Theorem

March 3, 2010 GB Compass and Ruler, High School Geometry, Software Tutorials

In the previous CaR tutorial, we constructed and isosceles triangle. In this tutorial we are going to explore the properties of the segment connecting the midpoints of its two sides. In this tutorial we are going to learn the following:

use the move tool, triangle tool and segment tool
find the midpoint of two a segment
measure angles using the angle tool
edit properties and reveal measures of angles and segments

Construction Steps

	1.) Open CaR. We will not need the Coordinate axes so click the Show grid icon until the Show the Grid icon until the grid or axes is not shown.
	2.) Click the Triangle tool and click three different points on the drawing pad.
	3.) Click the Move tool and right click one of the points to display the Edit Point dialog box. In the Name text box, change the name to A, then click the Show object names button (enclosed with red ellipse in Figure 1). Figure 1 – The Edit Point dialog box.
	4.) Change the name of the other two points to B and C.
	5.) Click the midpoint tool, click point A and click point B to get the midpoint of AB. Now, get the midpoint of BC. Rename the midpoint of AB to E and the midpoint of AC to F (Refer to step 3). Your drawing should look like Figure 2. Figure 2 – Triangle ABC with midpoints D and E.
	6.) Right click and drag the labels to adjust their positions. Using the Move tool, move the vertices of the triangle. What do you observe?
	7.) We will see the relationship of the angles and the segments in triangle ABC. We will measure the angle first. To measure angle ADE, click the points in the following order: point A, point B and point C. After this step, you will see the angle symbol at angle *ADE*.
	8.) To display the measure of the angle, click the Move tool and right click the angle symbol. This will display the Edit Angle dialog box shown in Figure 2.
	9.) To display the measure of the angle, click the Show object values icon. Then click the smallest angle symbol size to reduce the angle size. Now, click the OK button to apply changes. Figure 3 – The Edit Angle dialog box.
	10.) Using step 8-9, measure angles *ABC, ACB* and *AED*. After measuring, your drawing should look like the figure below.
	11.) Using the Move tool, drag the vertices of the triangle. What do you observe?
	12.) Based on the measures of the angles shown in your drawing, what can you say about segment DE and segment BC?
	13. ) Now, we will see if there is a relationship between the length of the segments in triangle *ABC. To reveal the measure of DE, use the Move tool* and right click the segment. This will reveal the Edit Line, Ray, Segment dialog box as shown in Figure 3. Figure 5 - The Edit Line, Ray, Segment dialog box.
	14.) In the Edit Line, Ray, Segment dialog box, click the Show object values button.
	15.) Using steps 13-14, display the length of segment BC.
	16.) What can you observe about the relationship of segments DE and BC?
	17.) Move the vertices of the triangle. Are your observations still the same?
	18.) Make a conjecture about your observations above.

One comment compass and ruler software, dynamic geometry, free, free math software, free software, midline theorem, midpoint of sides of a triangle

The Algebraic and Geometric Proofs of Pythagorean Theorem

February 3, 2010 GB High School Geometry, High School Mathematics

The Pythagorean Theorem states that if a right triangle has side lengths $a, b$ and $c$ , where $c$ is the hypotenuse, then the sum of the squares of the two shorter lengths is equal to the square of the length of the hypotenuse.

Figure 1 – A right triangle with side lengths a, b and c.

Putting it in equation form, we have

$a^2 + b^2 = c^2$ .

For example, if a right triangle has side lengths $5$ and $12$ , then the length of its hypotenuse is $13$ , since $c^2 = 5^2 + 12^2 \Rightarrow c = 13$ .

Exercise 1: What is the hypotenuse of the triangle with sides $1$ and $\sqrt{3}$ ?

The converse of the theorem is also true. If the side lengths of the triangle satisfy the equation $a^2 + b^2 = c^2$ , then the triangle is right. For instance, a triangle with side lengths $(3, 4, 5)$ satisfies the equation $3^2 + 4^2 = 5^2$ , therefore, it is a right triangle.

Geometrically, the Pythagorean theorem states that in a right triangle with sides $a, b$ and $c$ where $c$ is the hypotenuse, if three squares are constructed whose one of the sides are the sides of the triangle as shown in Figure 2, then the area of the two smaller squares when added equals the area of the largest square.

Figure 2 – The geometric interpretation of the Pythagorean theorem states that the area of the green square plus the area of the red square is equal to the area of the blue square.

One specific case is shown in Figure 3: the areas of the two smaller squares are $9$ and $16$ square units, and the area of the largest square is $25$ square units.

Exercise 2: Verify that the area of the largest square in Figure 3 is 25 square units by using the unit squares.

Figure 3 – A right triangle with side lengths 3, 4 and 5.

Similarly, triangles with side lengths $(7, 24, 25)$ and $(8, 15, 17)$ are right triangles. If the side lengths of a right triangle are all integers, we call them Pythagorean triples. Hence, $(7, 24, 25)$ and $(8, 15, 17)$ are Pythagorean triples.

Exercise 3: Give other examples of Pythagorean triples.

Exercise 4: Prove that there are infinitely many Pythagorean triples.

Proofs of the Pythagorean Theorem

There are more than 300 proofs of the Pythagorean theorem. More than 70 proofs are shown in tje Cut-The-Knot website. Shown below are two of the proofs. Note that in proving the Pythagorean theorem, we want to show that for any right triangle with hypotenuse $c$ , and sides $a$ , and $b$ , the following relationship holds: $a^2 + b^2 = c^2$ .

Geometric Proof

First, we draw a triangle with side lengths $a, b$ and $c$ as shown in Figure 1. Next, we create 4 triangles identical to it and using the triangles form a square with side lengths $a + b$ as shown in Figure 4-A. Notice that the area of the white square in Figure 4-A is $c^2$ .

Figure 4 – The Geometric proof of the Pythagorean theorem.

Rearranging the triangles, we can also form another square with the same side length as shown in Figure 4-B.This means that the area of the white square in the Figure 4-A is equal to the sum of the areas of the white squares in Figure 4-B (Why?). That is, $c^2 = a^2 + b^2$ which is exactly what we want to show. *And since we can always form a (big) square using four right triangles with any dimension (in higher mathematics, we say that we can choose arbitrary $a$ and $b$ as side lengths of a right triangle), this implies that the equation $a^2 + b^2 = c^2$ stated above is always true regardless of the size of the triangle.

Exercise 5: Prove that the quadrilateral with side length C in Figure 4-A is a square.

Algebraic Proof

In the second proof, we will now look at the yellow triangles instead of the squares. Consider Figure 4-A. We can compute the area of a square with side lengths $a + b$ using two methods: (1) we can square the side lengths and (2) we can add the area of the 4 congruent triangles and then add them to the area of the white square which is $c^2$ . If we let $A$ be the area of the square with side $b + a$ , then calculating we have

Method 1: $A = (b + a)^2 = b^2 + 2ab +a^2$

Method 2: $A = 4(1/2ab) + c^2 = 2ab + c^2$

Methods 1 and 2 calculated the area of the same square, therefore they must be equal. This means that we can equate both expressions. Equating we have,

$b^2 + 2ab + a^2 = 2ab + c^2 \Rightarrow a^2 + b^2 = c^2$

which is exactly what we want to show.

Leave a comment algebraic proofs, geometric proofs, proof of pythagorean theorem, pure mathematics, pythagora's theorem, pythagorean theorem, pythagorean triples, right heron triangles, right triangles

« 1 … 16 17 18 19 20 … 23 »